【项目实践】基于区块链的记账系统&Go语言学习

0 前言

本学期的区块链课程需要利用区块链的原理，自己实现一个电子帐本。反复查阅资料，我发现除了C++语言以外，Go语言在区块链系统和交易平台里相当常见——它以简洁语法、高效并发（goroutine）和卓越性能著称，适合构建高并发分布式系统，因此在这些应用中被广泛使用。

恰逢我最近明显感到“被Python惯坏了”，并因此有些焦虑，想要学习一些新的东西来打破舒适圈。于是灵机一动，决定用Go语言来完成区块链实验的项目。尽管我并不知道Go语言有些什么特性，甚至从未接触过这门语言，但我坚信掌握一门编程语言的最好方法是在实践中使用它。边做边学，我总能收获一些东西。

而对于区块链记账系统的实现，老师给出了实验步骤和大致思路（虽然又是Python版本的）。因此我只需分步骤完成每个模块的设计，再将它们整合起来就可以了。

为了帮助理解各个模块的功能，我也会大致介绍一下区块链的整体框架，然后再分别实现各个模块。

因此你将在这篇文章中看到：

• 区块链相关原理的简要阐述
• 我从0基础开始，逐步掌握一门编程语言的探索路径
• 构建一个基于区块链的记账项目的详细过程
• 区块链相关技术的Go实现

1 区块链技术要点简述

区块链的本质可以理解为一个公开透明、去中心化且防篡改的数据库。而由于区块链的出现，正是为了解决在缺乏信任中介的环境下，如何实现可信的记录和交易，也可以说区块链是一个在互不信任的参与者之间维系的记账技术。它使用的主要算法，都是以“去中心化”和“防篡改”作为核心目的的。而去中心化本身，就能够让数据具有一定的不可篡改性，因此两者也可以说是相辅相成的。

数据的组织形式

顾名思义，区块链的数据组织形式就是“打包成区块，再衔接成链”。数据首先被打包成一个个的区块（Block），然后通过哈希的形式链接起来，从而形成一条长链。

每个区块包含区块头和区块体。其中区块体则是被该区块打包的具体数据，而区块头则记录了这个区块的一些摘要信息，是区块能够构成链条的关键所在，包括版本号、前一个区块的哈希值、Merkle根哈希值、区块被创建的时间戳、难度目标和随机数Nonce。

接下来将对区块头中的各个变量逐一进行介绍。
版本号标识了该区块遵循的区块链协议的版本。这确保了网络中的所有节点能够正确地解析和验证该区块。

时间戳记录了该区块被创建的大致时间，它对于维护交易的顺序和区块链的时间序列至关重要。

前一个区块的哈希值是当前区块指向链上前一个区块的哈希指针。如果试图修改前一个区块的数据，其哈希值将改变，从而导致其后所有区块的哈希链接失效，因此可以迅速识别并拒绝这种篡改。通过包含前一个区块头的哈希值，每个新的区块都与前一个区块在密码学上链接起来，形成一个不可篡改的链条。这是区块链核心的结构性特征。
Merkle根哈希值用于概括和验证区块体中的数据。Merkle 树是一种基于哈希的数据结构，若当前区块中的某处数据被改动，则从对应叶节点到Merkel树根节点的哈希值都会发生改变。从根向下逐层寻找，就能定位到被篡改的记录。

难度目标和随机数则和用于建立共识的工作量证明算法有关，可以在后续进行了解。

以比特币为例，其区块链的区块结构如下所示。

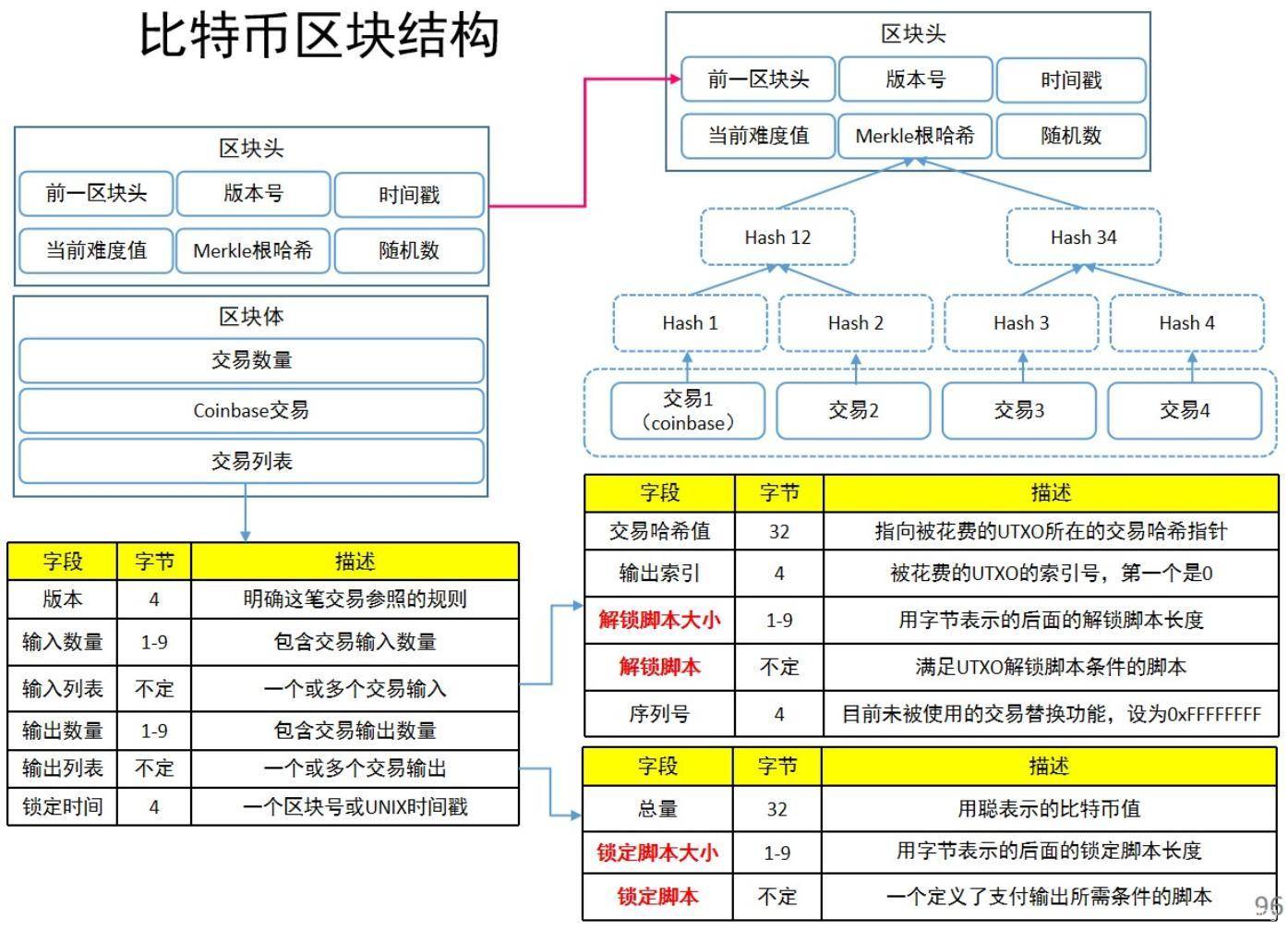
共识机制

去中心化意味着区块链网络的运行，并不依赖一个统一的管理机构；而为了保证防篡改，区块链网络中的每个节点都假定除了自己以外，其余所有节点都是不可信任的。这时就需要有一种方法，能够使这些没有信任基础的个体达成一致——我们称之为共识机制。

有了共识机制，网络中的各个节点得以同步彼此的交易和账本信息，并且让新生成的区块得到其他节点的认可。

常见的共识机制包括工作量证明（Proof-of-Work，PoW）、权益证明（Proof-of-Stake，PoS）等。工作量证明是比特币网络用于达成共识并验证新交易、创建新区块的核心机制，也就是我们常听说的“挖矿”所代表的实际工作。其基本原理是要求矿工通过进行大量的计算工作，解决一个密码学难题，来证明他们投入了足够的计算资源。

前文提到区块头中的两个值，难度目标和随机数即是控制与解决这一难题的关键变量。具体而言，PoW要求节点就是构造一个区块，其区块头的哈希值满足特定要求。具体的要求由区块头中的难度目标所决定。

难度目标表示了矿工在挖掘新区块时必须满足的难度级别。它决定了生成一个新的有效区块所需的计算量。区块链网络会根据一定的规则动态调整难度目标，以维持区块产生的稳定速率。

而Nonce值是一个在挖掘新区块时由矿工尝试的不同随机数值。矿工通过不断改变 Nonce 值并计算区块头的哈希值（Nonce改变，包含Nonce的区块头哈希值也随着改变），直到找到一个满足难度目标要求的哈希值。一旦找到符合条件的 Nonce 值，新的区块就被创建并添加到区块链中。

这样的计算难题难以解决，但验证起来很容易（算一遍区块头的哈希值是否符合实际即可），便于所有节点达成共识。也就是说，当一个节点通过投入算力，完成了这个密码学难题，它就具备了新增区块的资格，能够被其他节点所信任——相当于力大飞砖，用算力硬核堆出的认可。

当然，其他节点仍需验证该区块是否合法（如交易是否双花、格式是否正确等），验证通过后才会接受。

而节点间的“共识”则体现在“最长链原则”上。确切地说，最长链指的是“最大累计难度链”，即所有节点都会选择在当前累计工作量最多的链上工作，并仅接受最长链末端新提交的区块。

而区块链的防篡改性也得益于这一原则。因为一旦需要篡改某个区块，就需要重新完成该区块及其之后所有区块的工作量证明，并且保证伪造链的长度比当前的正常链还要长。这会消耗巨大的算力，在经济上也不可行。

因此，信息一旦上链，就难以篡改（其余矿工的持续工作、区块链的持续延长会阻止这一事件的发生），并且随着时间的推移，其篡改难度会不断升高。

当然，算力并不是免费的。为了维持共识，需要引入一定的经济激励。而矿工通过付出计算资源（工作量）来获得奖励，就像是买彩票一样。由于区块链通常伴随着虚拟加密货币体系，挖矿被赋予了实际的经济价值，因此这一共识机制得以自洽。

此外，就算有了共识机制的存在，“意见不统一”的情况还是常有发生。例如区块链的分叉现象，指的是多个矿工几乎同时挖出新区块，导致链条一时出现“分裂”的情况。此类情况如何解决，也是共识机制中的重要内容，感兴趣的同学可以进一步了解“软分叉”与“硬分叉”的区别。

共识机制是区块链在去中心化架构下，得以成立并发挥作用的最核心要素之一，也是维护链式区块这一数据结构的关键引擎。 可以说将它理解透了，就基本掌握了区块链技术。也正因如此，笔者无法在这里将所有的技术细节都介绍清楚，只能按着自己的理解大致介绍。若有疑问，欢迎在评论区讨论。

从数字货币到分布式应用

区块链的概念自2009年随着比特币网络的应用被提出，其自身也在不断发展。上面所介绍的技术皆属于最初的区块链，即区块链1.0。其核心应用就是电子帐本，技术架构如下所示。

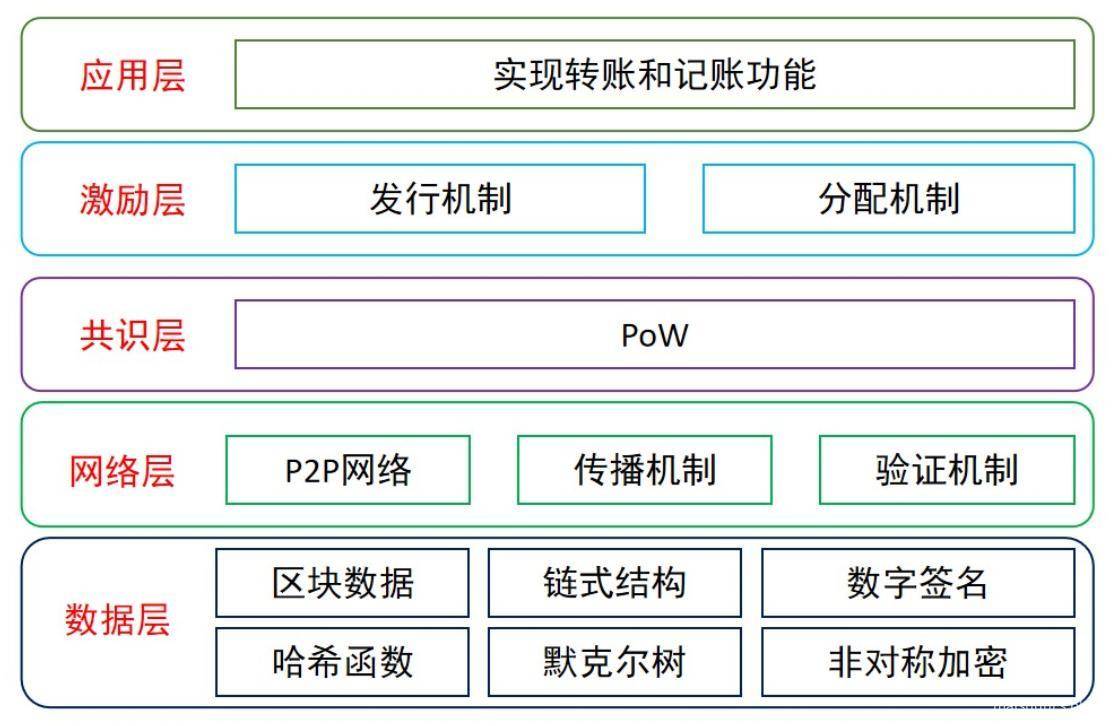
而在比特币大火之后，越来越多的人意识到了区块链技术的价值，并将其应用拓展到了整个金融行业乃至更广阔的领域，例如分布式身份认证、分布式域名系统等应用。区块链2.0应运而生，智能合约的出现，允许在区块链上进行分布式的编程，支持商业环境下的各种合约需求。

关于区块链的介绍就到这里。接下来就是大众喜闻乐见的动手部分了。

2 环境配置与Hello World!

Go环境的配置并不复杂，从官网下载对应版本的安装包，直接安装就行了。接着简单配置环境变量，就能在命令行编译运行Go程序。我选择在VS Code作为IDE，因此还需要安装相关插件和配置。此处不再赘述。

我参考了这篇文章配置 VS Code 的Go开发环境。当然在配置完成之后也遇到了一些问题（提示go.mod file not found），最终在CSDN上找到了问题的解决方案，有类似问题的同学也可以参考一下。感谢这些分享经验的作者❤。

接下来就是大众更加喜闻乐见的 Hello World 时间。编译运行，看到对应字符串就说明环境配置成功了。

package main
import "fmt"

func main() {
    fmt.Println("Hello, World!")
}

我不喜欢跟着视频或者网课学习，因此接下来几乎所有关于Go的语法和特性，我都是从菜鸟教程上学习的，偶遇一些困难再针对性地用搜索引擎。除此之外，我尽量避免使用AI工具直接生成代码，不仅形成路径依赖，自己也什么都学不到。

3 Merkle树的生成

Merkle树（Merkle Tree）是一种基于哈希的二叉树结构，用于高效验证大规模数据的完整性与一致性。其核心思想是将数据块逐层哈希，最终生成一个根哈希值（Merkle Root），任何数据的篡改都会导致根哈希变化。Merkle树是区块链的核心结构，区块头中的Merkle树根保证了区块内数据不被轻易篡改。

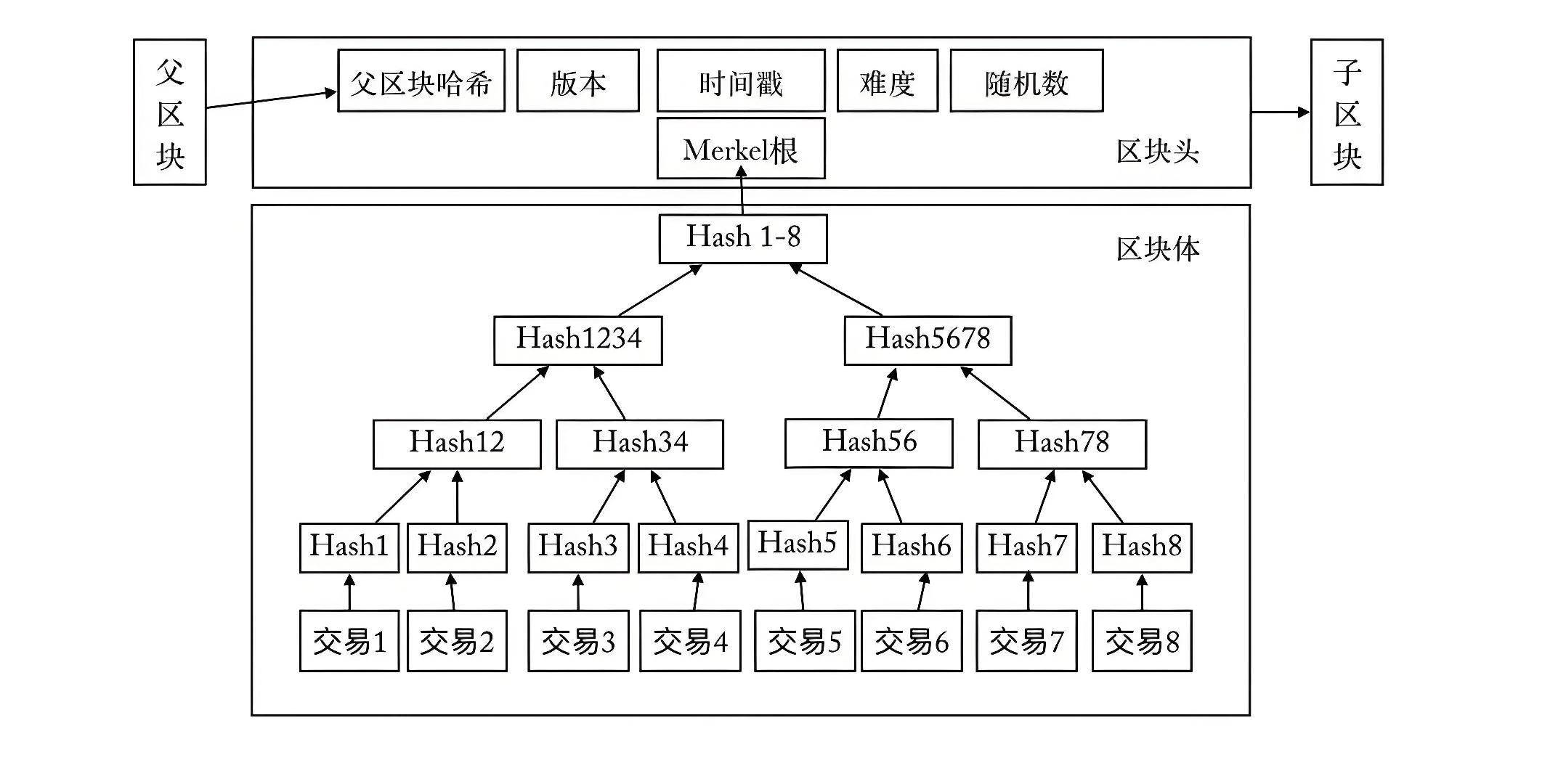
然而初来乍到，对Go语言的各种特性、程序设计思想都不清楚，就算知道Merkle树的结构和实现，我还是感到无从下手。甚至查了资料之后，我才知道Go中没有“类”的概念，只有结构体，更不用谈按以前的老路子，用面向对象的思想设计一个结构清晰的程序了。

不知道从什么时候开始养成了不写类就不会写程序的坏习惯……非得从头把整体架构设计好，把程序好好封装起来不可。

既然如此，那就不妨把事情做得简单粗暴一点——直接像C程序那样从头到尾地写，不管代码易读性和可扩展性啥的，先实现功能再说。毕竟基础的声明、循环、条件判断语句都是一样的，只是语法略有不同罢了。说干就干，先把程序逻辑用文字表述出来。

数据块的结构体定义 可包括交易内容，先用一个简单字符串代替；

Merkle树节点的定义 {
    指向数据块的指针
    节点的哈希
    左右子节点的指针
}

函数：构建Merkle树
    传入参数：当前待处理数据列表
    返回参数：根节点，指向处理完成的Merkle树
    函数过程：
        由于Merkle树自下而上生长，根据数据列表创建叶节点。
        最终得到一个完全由叶节点构成的节点列表。
        调用递归函数，传入节点列表，使节点两两合并，计算哈希。
        再递归函数中递归向上构建树，递归完成后，得到根节点指针

函数：递归构建过程
    传入参数：Merkle结点指针列表
    返回参数：Merkle结点指针列表，是合并后的产生的父节点列表，层数-1
    递归边界：节点列表中只有一个元素，说明已经生成了根节点
    函数过程：
        判断递归边界
        创建一个用于下一步递归的父结点列表
        遍历传入的节点列表，若传入参数中还有未处理的节点：
            创建一个新的结点表示父节点
            从传入参数中取2个结点（若只剩下一个则只取最后一个）
            用子结点地址更新父结点的左右指针，计算Hash值更新父节点Hash
            将父节点指针放入列表中
        递归调用函数，将新构造的父结点列表传入，并将递归函数的返回值返回

函数：计算哈希
    传入参数：1个Merkle树节点的指针
    返回参数：SHA256哈希值
    函数过程：
        若传入的节点具有两个子节点，则取它们的哈希值相连接，再计算Hash
        若只有左子节点，则取它的哈希值，再计算一次Hash
        若不具备子节点（有数据块），根据数据块的内容计算Hash

一边查资料一边写，花了小半个晚上终于写出来且运行成功了。

package main

import (
    "crypto/sha256"
    "fmt"
)

type DataBlock struct {
    content string
}

// Merkle树节点定义
type MerkleNode struct {
    data        *DataBlock
    hash        string
    left_child  *MerkleNode
    right_child *MerkleNode
}
  
// 从数据块构建Merkle树，返回根
func create_tree(datas []DataBlock) MerkleNode {
    var nodes []MerkleNode
    // 遍历所有数据块，创建叶节点
    for _, data := range datas {
        var newNode MerkleNode
        newNode.data = &data
        update_hash(&newNode)
  
        nodes = append(nodes, newNode)
    }
    return build_tree(nodes)[0]
}
  
// 递归逐层构建Merkle树
func build_tree(sons []MerkleNode) []MerkleNode {
    var fathers []MerkleNode
    // 相邻节点配对，创建它们的父节点
    for i := 0; i < len(sons); i += 2 {
        var newNode MerkleNode
  
        newNode.left_child = &sons[i]
        if i+1 < len(sons) {
            newNode.right_child = &sons[i+1]
        }
        update_hash(&newNode)
  
        fathers = append(fathers, newNode)
    }
  
    if len(fathers) == 1 {
        return fathers
    } else {
        return build_tree(fathers)
    }
}
  
// 根据子节点信息，计算当前节点Hash
func update_hash(node *MerkleNode) {
    hash := sha256.New()
  
    // 存在data，说明是叶节点
    // 否则根据左右子节点的哈希计算
    if node.data != nil {
        // 若指向数据块，根据content属性计算哈希值
        hash.Write([]byte(node.data.content))
    } else {
        hash.Write([]byte(node.left_child.hash))
        if node.right_child != nil {
            hash.Write([]byte(node.right_child.hash))
        }
    }
    node.hash = string(hash.Sum(nil))
}
  
func main() {
    datas := [5]DataBlock{{"ha"}, {"hello"}, {"world"}, {"aaa"}, {"hello~"}}
    root := create_tree(datas[:])
    fmt.Printf("Root Hash of Merkle Tree:%x\n", root.hash)
}
  
/*
参考链接：
    - https://blog.csdn.net/qq756684177/article/details/81518823
    - https://www.cnblogs.com/X-knight/p/9142622.html
    - https://zhuanlan.zhihu.com/p/666478154
    - https://www.cnblogs.com/wanghui-garcia/p/10452431.html
*/

（为了节省篇幅，之后实现的代码不再全部放出）

运行程序，得到了根的哈希值如下。

Root Hash of Merkle Tree: 0459318b3f497cfcf068757a40c06a821e3cf1894682cbec23a3630dfa236986

在写的过程中，我通常是需要用什么就去找什么。例如，想知道如何定义一个变量，我就把变量声明相关的章节看了一遍，然后自己选取合适的方法往下写。因为各个编程语言都是相通的，因此我只要把语法习惯改过来，很快就能上手。

（小声吐槽，从来没有把类型写在变量名/形参后面过，真的好不习惯……）

但是这样会遇到一个问题——有一些Go语言特有的特性是我事先不知道的，于是我就会用一些比较绕的思路去解决原本很简单的问题。

例如在第22行声明MerkleNode数组时，我一开始的思路是先获取输入数据块的数量，再申请相应大小的数组，然后用循环变量逐个填入叶节点。但后来我发现除了固定长度的数组之外，Go提供了一种可变长度的数据结构，切片——我可以方便地使用append方法在切片后追加元素，这样就避免了上述的复杂写法，但也产生了一些返工。

var nodes []MerkleNode                   // 声明一个切片，存储父节点
    for _, data := range datas {
        var newNode MerkleNode
        nodes = append(nodes, newNode)   // 将新节点加入到切片中
    }

面对这种情况，我采取的方案是从别的高级语言中“迁移”过来一些思考模式。例如，在写上面的for循环时，我就想到Python中，可以对列表简单地使用类似 for element in list 的形式快速取出元素。于是我以“迭代”作为关键词搜索，发现果然在Go中也存在类似的特性——range关键字。

当然这种方法的前提是学习过Python、Java等主流高级语言，知道哪些时候能够有更简略的写法。

除此之外，第一次写Go，难免有些磕磕绊绊，代码中也有很多用法不一致的地方。于是请到了手下的外籍员工帮我检查一下代码规范（误）。

总而言之，第一次尝试还是很成功的，学会了Go的基本语法（虽然还很不熟练，远远谈不上掌握），也了解了range关键字、切片等特性，算是成功入了门。

---

目前完成的进度就到这里，接下来需要完成的工作：

• 比特币的工作量证明PoW算法
• 椭圆曲线密码的公钥和私钥生成，并通过编码生成比特币的公钥地址
• 连接数据库，并将比特币公钥和公钥地址存入数据库